Whether you’re conducting research, reading about research, or learning research methods so you can ace your research methods course, you need to know exactly what a confounding variable is. If you think you’ve got it, then this isn’t the post for you. But if you’re confounded by the idea of a confound, then this post may help you to see the light.
A somewhat formal definition of a confounding variable is “an extraneous variable in an experimental design that correlates with both the dependent and independent variables”. This is a terrible definition, full of words and phrases that mean nothing to 99% of the population. So, let’s start with a classic concrete example.
AN OLD CLASSIC: MURDER AND ICE CREAM
It is known that throughout the year, murder rates and ice cream sales are highly positively correlated. That is, as murder rates rise, so does the sale of ice cream. There are three possible explanations for this correlation:
Possibility #1: Murders cause people to purchase ice cream. One could imagine a world where this is true. Perhaps when one is murdered, they are resurrected as zombies who primarily feed on ice cream.
Possibility #2: Purchasing ice cream causes people to murder or get murdered. Again, one could imagine a world where this is true. Perhaps when one eats ice cream, those without ice cream become jealous and murder those with ice cream.
Possibility #3: There is a third variable—a confounding variable—which causes the increase in BOTH ice cream sales AND murder rates. For instance, the weather. When it’s cold and Wintery, people stay at home rather than go outside and murder people. They also probably don’t eat a lot of ice cream. When it’s hot and Summery, people spend more time outside interacting with each other, and hence are more likely to get into the kinds of situations that lead to murder. They are also probably buying ice cream, because nothing beats the sound of an ice cream truck on a blazing Summer day.
In this example, the weather is a variable that confounds the relationship between ice cream sales and murder rates. You may also recognize this as the so-called third variable problem, which refers to the fact that any time we observe a relationship among two variables, there’s always the possibility that some third variable which we don’t know about is responsible for (“confounding”) the relationship.
A CONCRETE EXAMPLE WITH A PRETTY PICTURE
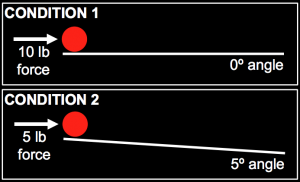
If you still don’t get it, I’ve got another example and a pretty picture to go with it. Imagine you’d like to examine the relationship between the force you apply to a ball and the distance the ball travels. Naturally, you predict that the more force you apply, the further the ball will travel. You create an experiment with two conditions. Now you should be eyeballing that pretty picture I told you about. In Condition 1, you apply a 10 lb force to the ball and measure the distance traveled. In Condition 2, you apply a 5 lb force to the ball and measure the distance traveled. After you run your experiment, you observe that the ball travels further in Condition 2 than it does in Condition 1. In other words, you find that the less force you apply, the further the ball travels. Should you conclude that Isaac Newton was wrong? No. As should be pretty clear from that pretty picture, there’s a clear confounding variable in this experimental design: the angle of the slope. Given the presence of this confound, we have no way of knowing which variable – force or angle – is responsible for the change in the distance the ball travels.
This illustrates why it’s so important to always be on the lookout for confounds. Confounds can make us reach conclusions that are wrong; confounds can make us look stupid. Or, to use slightly more technical language: confounding variable = BAD.